Music and Mathematics:
The Common Structure of
Musical Intervals and Natural Numbers

Note to the Mathematically inclined: The structural commonality described below between musical intervals and natural numbers are intended to illustrate the necessity of changing the skill development priorities for the study of music theory so that it alignes (to its benefit) with the skill development priorities in the study of elementary arithmetic. I am not claiming that music theory, insofar as it handles pitch, is a formal system by the standards applied to mathematical and logical systems. Although it is true that there are very interesting commonalities of structure that deserve further exploration, not all of which are described in this article.

------------------------------------------------------------

The structural observation described here is the basis for an insight that lead to the development of the fastest and most effective method for learning to spell musical intervals.

My experience in providing R&D services for the development of a very effective multiplication course led me to first reflect on the importance of accelerating basic skill development. The method invovled allowed us to teach single digit multiplication to second graders in one day with class averages of over 90% (yes, that is the class average, not the highest score) When I saw that students could learn mathematics much faster and with much better performance than occurs with traditional methods, I was led to an important realization. Students who develop a high degree of competence in essential skills early will have a superior developmental path throughout their study of mathematics. These essential skills involved the simple manipulation of numbers. 

While I was developing mathematics and music courses that have been used in schools all over the United States and internationally, I recognized that musical intervals are also numbers within the constraints of our 12 tone equal temperament musical system (an important qualitfication). Not only do musical intervals function like numbers with regard to measuring and manipulating differences of pitch in the creation of music, their frequency ranges (measured in half steps) fit into the set structure proposed by Von Neumann's definition of ordinal numbers exactly like natural numbers. This means that musical intervals are structurally identical, in an important way within the relative scope of their function in our system of music, to natural numbers. This is different from how music is typically described as being "mathematical." Usually music is seen as mathematical because it is very easily amenable to being described mathematically.  However, at that level music is no more mathematical than an orange, which can also be described mathematically. This idea shows that music is mathematical because, relative to handling pitch, it has a structural identity common to mathematical systems such that it applies operations to a number like structure just like our basic mathematics with numbers. Musical intervals share an extrodinary structural identity with natural numbers; and therefore the skill development priorities of basic mathematics regarding the handling of numbers are very useful to the study of music theory. The basic insight of this course is that learning to spell intervals is just as fundamental to music theory's handling of pitch as learning to count is to basic mathematics. Because intervals are so fundamental to the handling of pitch differences in music, if you develop superior skill at spelling intervals, you will develop a superior capacity (relative to your own aptitude) to study music theory. This insight is not new, however the emphasis of priority I wish to convey is higher than is typically expressed in music education because it borrows the skill development priorities of the study of arithmetic.

The skill development priority of learning to count first, which I imported from the teaching of basic mathematics, is usually overlooked in music. The reason is that counting numbers in mathematics is fairly easy with an innate logic that allows people to embrace the learning of counting with ease. Spelling intervals, which is the musical analogue of counting, is not so easy. If you learn the spelling of intervals through rote memorization, there are over 450 specific facts to learn. More importantly, the notation of pitches and intervals have a less obvious logic that tends to inhibit easy rote memorization of interval spelling. This is why I created a mental musical interval calculator in order to conform the skill development priorities of the study of music theory to the skill development priorities of the study of basic mathematics.

Illustrating the Common Structure of
Musical Intervals and Natural Numbers

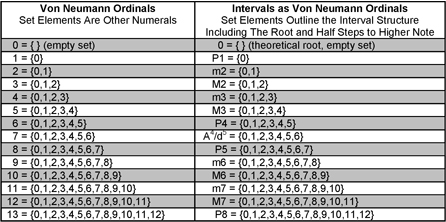
For the purpose of illustrating this structural commonality, I chose to use the set structure of a common definition of number. The mathematician John Von Neumann (1923) proposed that ordinal numbers, which include natural numbers, are sets that can be progressively pulled out of the empty set with a simple algorithm. I mapped the frequency ranges of the musical intervals into the ordinal set structure proposed by Von Neumann and found an interesting similarity. I do not claim that musical intervals ARE Von Neumann ordinal numbers. This comparison is simply to illustrate an exact commonality of structure. The frequency mapping assumed 12 tone equal temperament tuning and the measurement of pitch differences in half steps. In the chart below, each set representing an interval is a representation of the frequency range of the interval as measured in half steps. It contains a representation of the theoretical root frequency (0), which is the analogue to the empty set, and contains numbers representing each half step to the higher note in the specified interval. I found that the frequency ranges of musical intervals, as measured in half steps, fit into Von Neumann’s set based definition of ordinal numbers exactly the same as natural numbers.

On the right hand side of the table below, the musical intervals are listed from smaller to larger like the mathematical numerals on the left. On the right, zero (0) is a set that contains the theoretical root of any musical interval as its only member. If intervals are musical numbers and each interval has two notes that define a frequency range, then the theoretical root being a single frequency with a range of zero makes a good musical analogue for the empty set. Since the root (0) is needed to define the beginning of each interval’s frequency range, the root (0) must be the first element of each interval set just like zero in Von Neumann’s ordinal number sets. The P1 (Perfect Prime) interval, which is a musical analogue for the Von Neumann ordinal number one, is made up of two notes that are instances of the same theoretical root and is thus like a set containing the empty set. This is because, even though there are two notes in a P1, the distance in frequency between two instances of the same frequency is zero, just like the empty set that contains the theoretical root. The other numbers in each set represent the first (1), second (2), third (3), etcetera, half steps above the root (0). The last and highest number in each set on the right represents the highest half step above the root and the end point of that interval’s frequency range, which is the higher note. The highest number in each set is also the total half step count for that interval. A Major 3rd (M3 = {0,1,2,3,4} ) for example, has a frequency range of four half steps above its root.

According to Von Neumann’s definition of ordinal numbers, it is true for every number that:

 (Speaking of the number X as its set) set X is an ordinal only if X is completely ordered with regard to subset relationships and each element of X is also a subset of X.

 To see what this means, look at the left hand side of the table above. For example, 3 is a set element of 4 {0,1,2,3}. Since 3 = {0,1,2} then {0,1,2} is also a subset of {0,1,2,3}. This means that every set element of X is also an ordinal. This is true of all natural numbers, but may appear to not be true of musical intervals if we are looking at the interval names. This is because interval names such as P1 or M3 are not elements in any of the sets. Does this mean that the musical intervals cannot have a structure in common with Von Neumann ordinals?

 No. Interval names are just arbitrary symbols. The fact that the naming convention of the intervals is not consistent with the notation of their set elements is just semantics and does not say anything meaningful about the ordinal-like structure of musical intervals. Mathematical numerals are the same symbols used to represent their ordinal set elements. This allows the numeral names to show up in the sets. The numeral 3 can show up in sets of higher numbers as the set element 3. Thus the names of mathematical numerals fit in with the set structure of Von Neumann’s ordinal numbers. Interval names are derived from an arbitrary convention that combines a number and a word. The names in the table are just abbreviations. If we simply renamed the intervals of P1 through P8 with the equally arbitrary names of 1 through 13,[1] we can see that musical intervals fit into this set structure exactly like natural numbers, because the names of the intervals are now consistent with the arbitrary naming convention of their frequency ranges and obviously fit into the set structure of Von Neumann’s definition of ordinal numbers.  

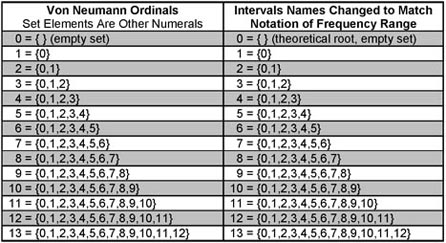
With the renamed intervals, you can see that the musical intervals exactly match the ordinal structure of natural numbers as defined by Von Neumann. It is also true for all ordinals that every ordinal number X is a set, whose elements are all the numbers smaller than X. This also shows that the frequency ranges of musical intervals have an ordinal structure. However, musical intervals are not similar to numbers just because we recognize their ordinal structure. An important part of understanding the amazing contribution that differences in pitch make to the value and meaning of music involves measuring those differences. The way we measure those differences in our twelve tone equal temperament system is through intervals. Intervals stand at the center of musical creation and interpretation in way that embodies the heart of how numbers function in a mathematical system. That this structure is common to both music and mathematics shows that music is mathematical in a systemically functioning sense such that operations are applied to numbers in both systems.

If there is a way that musical intervals are not numbers in a mathematical sense, it will have to do with the existence of powerful differences between our systems of music and mathematics. Mathematics is an imaginary system that can easily be applied to all kinds of imaginary and real things. Music, as it pertains to intervals, is a system based on the actual measures of a real and very specific physical phenomenon (pitch) and is not well applied to imaginary things. Our system of mathematics is infinite. There are an infinite set of numbers, as well as an infinite number of decimal places between each adjacent pair of numbers. This gives mathematics an ability to count, measure and calculate that exceeds the limits of the universe. Music is very finite. There is a finite set of possible intervals that are defined by the physical structure of pitch frequencies and are further limited by the range of human hearing and the preferences of human aesthetic sensibilities. Between any two pitches that are one half step apart, there is a practical division of only one hundred frequencies (called cents). The human ear can only distinguish differences in frequency that are a minimum of five one hundredths of a half step (five cents). There are real reasons that result from the limited scope of pitch, the furthur limitation of human hearing, and the even furthur limitation of human aesthetic preferences, through which musical intervals will not have the same capacities or characteristics as numbers in our mathematical system. Another question is that the rules of music theory may not be sufficient to constitute a formal system in the mathematical-logical sense.

However, to the extent that intervals function within the constraints of the twelve tone equal temperament musical system, intervals function with enough structural similarity to mathematical numbers as to be the numbers of our pitch based music. Both music and mathematics use a set of basic elements (intervals, numbers) that have an ordinal structure. Both systems have operations that are applied to these elements. Most importantly, our progress in the study of both music and mathematics benefits from skill development pertaining to the simple manipulation of each system’s set of numerals. It is the observation that the structure and function of number exists in both music and mathematics, which provides the skill development focus of this course. In mathematics there is a very clear focus on essential skill development relative to working with numbers. The undeniable clarity of the structure and function of numbers in mathematics enforces the priority of this focus and the resulting sequencing of subject matter in course design.

A great deal of music education lacks this focus. Relative to the scope of music, the structure and function of number exists in music in a very similar way to how it exists in mathematics. Therefore, a similar priority of focus on skill development in music education is appropriate. In mathematics, you would not dream of teaching more advance topics without first teaching a student how to count. The musical equivalent of counting, which is spelling intervals, is often put off for years or never developed at all. Musical counting, to the detriment of music students, is almost never developed to anywhere near its full potential. In order to bring essential skill development for music theory in line with the developmental dictates of the numerical structure of musical intervals, The Music Theory Advantage^TM course of study will prioritize a focus on developing your skill in working with musical intervals in order to enhance your productivity in the study of music theory. This will serve to develop a set of essential skills that are the musical analogue of counting.