Max Maxwell
This is an example of the "Modern Socratic Method" taken from Plato's Meno. This type of questioning is characterized by the fact that answers to the questions are knowable. This type of question stands in contrast to questions in the "Classic Socratic Method", which are unknowable or are unverifiable, such as "What is Justice?". Plato thought the geometry focus in his dialogue Meno was an illustration of his idea that all knowledge is recollection. Plato's explicit thought in this dialogue is that the boy is able to answer because he remembers what he already knew. Occam's razor leads us to consider that the boy is able to answer because people are able to make all kinds of intelligent inferences concerning what they did not know when under the influence of carefully leading questions.
Leading students, through questions, to do their own thinking about a specific objective presupposes there is some knowledge in the student to form the basis for answering questions. In the dialogue below, the boy already knows what a square and diagonal are and can do basic calculation. The purpose of my use of this example is not to affirm Plato's theory of recollection nor to state that the questions involved in the example below are the way to approach this particular subject. It's purpose is to show you how simple it can be to lead someone in their thinking about a primary question or objective through leading questions.
Unlike the "Classic Socratic Method" in which the goal is to cause a person to refute their own beliefs about questions, whose answers are unverifiable and amazingly unpredictable. The Modern Socratic Method is easier to implement in a planned and common sense fashion because all answers to all questions are knowable and verifiable. If you are reading this because you want to learn to use the Socratic method, you must realize that all importance must be place on the psychological state of your students. Experiences of the Socratic method that make people more uncomfortable with asking and answering questions are worthless. The Socratic goal we should embrace is the goal of making students more interested in asking questions and doing their own thinking. See the essay "How to Use the Socratic Method" for more information the primary social dynamic needed for the implementation of the Socratic method in a classroom or for one on one dialogue.
In the example below, the goal is to find how to construct a square exactly twice the size of the original square. This example is simply guided observation along with questions that help the respondent to make easy to reach inferences. This excerpt occurs in the middle of Plato's Meno. (Stephanus number 84d)
Excerpt from the Geometry dialogue in Meno:
(illustrations are mine)
Socrates: Tell me, boy, is not this a square of four feet which I have drawn?
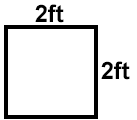
Boy: Yes.
Socrates: And now I add another square equal to the former one?
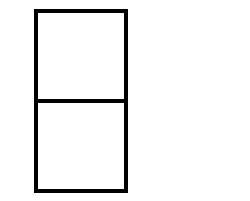
Boy: Yes.
Socrates: And a third, which is equal to either of them?

Boy: Yes.
Socrates: Suppose that we fill up the vacant corner?

Boy: Very good.
Socrates: Here, then, there are four equal spaces (squares)?
Boy: Yes.
Socrates: And how many times larger is this space than this other?
Boy: Four times.
Socrates: But it ought to have been twice only, as you will remember.
(the goal of making a square twice the size was stated earlier in the dialogue)
Boy: True.
Socrates: And does not this line (the blue line cutting the fours squares across the diagonal), reaching from corner to corner, bisect each of these spaces?
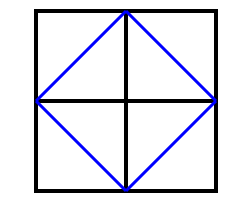
Boy: Yes.
Socrates: And are there not here four equal lines which contain this space (square made of the blue lines)?
Boy: There are.
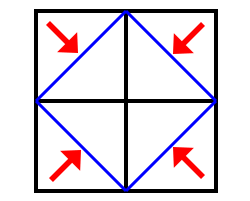
Socrates: Look and see how much this space is.
Boy: I do not understand.
Socrates: Has not each interior line (the blue line) cut off half of the four spaces?
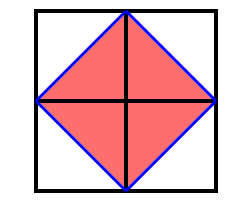
Boy: Yes.
Socrates: And how many spaces are there in this section
('spaces' are now refering to triangles in the square made of blue lines)?
Boy: Four.
Socrates: And how many in this?

Boy: Two.
Socrates: And four is how many times two?
Boy: Twice.
Socrates: And this space (square made of blue lines) is of how many feet?
Boy: Of eight feet.
Socrates: And from what line do you get this figure?
Boy: From this.
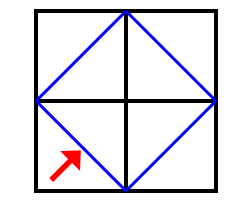
Socrates: That is, from the (blue) line which extends from corner to corner of the figure of four feet?
Boy: Yes.
Socrates: And that is the line which the learned call the diagonal. And if this is the proper name, then you, Meno's slave, are prepared to affirm that the double space is the square of the diagonal?
Boy: Certainly, Socrates.
Socrates: What do you say of him, Meno? Were not all these answers given out of his own head?
Meno: Yes, they were all his own.